Exercises on differential equation¶
The pendulum equation¶
We consider the equation
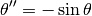
Write a function that returns an array containing the position and the angular velocity of the pendulum for  instants
instants 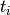 between 0 and
between 0 and 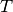 .
.
The initial position is  . Plot the phase space trajectory for different values of the initial velocity. Angle will be represented between -π and π.
. Plot the phase space trajectory for different values of the initial velocity. Angle will be represented between -π and π.
Solving the Schrödinger equation using the finite element method¶
Let us consider the Schrödinger equation with hbar = m = 1

The potential is 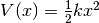 with
with 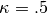 .
.
To solve the equation, we will truncate the x-axis to values between  and
and
 . We will also discretize the x-axis with small steps (
. We will also discretize the x-axis with small steps (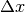 ).
).
The term 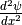 will be approximated using
will be approximated using 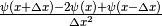 .
.
For the initial state, we will take a Gaussian distribution 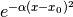 . We will use
. We will use 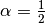 and
and 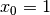 .
.
Calculate and plot 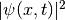 as a function of
as a function of  for
for 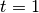 using the zvode solver with an absolute precision of
using the zvode solver with an absolute precision of 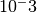 .
.