Exercises on graphics (and numpy)¶

Measurement of pi (Monte Carlo)¶

This exercise can be solved without any loop.

Using the rand function, creates two array X and Y with N=1000 random samples from a uniform distribution over [-1, 1[.
Plot the points
Plot a circle of radius 1 and plot using a different color the points inside the circle.
How many points are inside the circle ?
The number of points is proportional to the area of the circle. Deduce an approximate value of 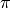$\pi$ . One can use 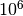$10^6$ points (without plotting the figure...)

Bode plot¶

The transfer function of a damped oscillator can written in the Fourier space using the formula :

$H(\omega) = \frac{\omega_0^2}{\omega_0^2 - \omega^2 + 2j\zeta\omega\omega_0}$

We would like to draw the three following graphs :

Bode plot for 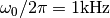$\omega_0/2\pi = 1 \mathrm{kHz}$ and $\zeta=0.1$
Tranfer amplitude function for 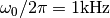$\omega_0/2\pi = 1 \mathrm{kHz}$ and different values of $\zeta$ .
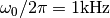Bode plot for the product of two tranfer function $\omega_0/2\pi = 1 \mathrm{kHz}$ , $\zeta=0.5$ , $\omega_1/2\pi = 2 \mathrm{kHz}$ , $\zeta=0.5$ .

You will uses the following functions :

loglog
semilogx
xlabel, ylabel et title
grid
subplot(ny, nx, n)
The label optional parameter and the function legend.
The angle function of numpy can be used to calculate the phase of a complex number. For the last graph, one should modify the phase in order for the plot to be continuous (do it without any loop!).

You should also know how to

make a string with accents (for french labels!).
format a string to insert parameters
For the greek letters, one can use unicode or latex formula.

Table Of Contents

Exercises on graphics (and numpy)
- Measurement of pi (Monte Carlo)
- Bode plot

Previous topic

Graphics in Python

Next topic

This Page