Exercises on graphics (and numpy)

Measurement of pi (Monte Carlo)

This exercise can be solved without any loop.

• Using the rand function, creates two array X and Y with N=1000 random samples from a uniform distribution over [-1, 1[.
• Plot the points
• Plot a circle of radius 1 and plot using a different color the points inside the circle.
• How many points are inside the circle ?
• The number of points is proportional to the area of the circle. Deduce an approximate value of 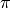. One can use 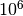points (without plotting the figure...)

Solution

from numpy import *
from pylab import *
ion()

N = 1000
X = 2*rand(N)-1
Y = 2*rand(N)-1

figure(1)
clf()
plot(X,Y, '.')
cond = (X**2 + Y**2)<1
plot(X[cond],Y[cond], '.')
theta = linspace(0, 2*pi, 201)
plot(sin(theta), cos(theta))

def mesure_pi(N):
    X = 2*rand(N)-1
    Y = 2*rand(N)-1
    Nb_points = sum((X**2 + Y**2)<1)
    return 4*Nb_points/float(N)

print mesure_pi(1000000)

Bode plot

The transfer function of a damped oscillator can written in the Fourier space using the formula :

We would like to draw the three following graphs :

• Bode plot for 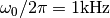and

  

• Tranfer amplitude function for 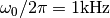and different values of .

  

• Bode plot for the product of two tranfer function , , , .

  

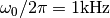You will uses the following functions :

• loglog
• semilogx
• xlabel, ylabel et title
• grid
• subplot(ny, nx, n)
• The label optional parameter and the function legend.
• The angle function of numpy can be used to calculate the phase of a complex number. For the last graph, one should modify the phase in order for the plot to be continuous (do it without any loop!).

You should also know how to

• make a string with accents (for french labels!).
• format a string to insert parameters
• For the greek letters, one can use unicode or latex formula.

Solution

from pylab import *

def H(omega, omega_0, zeta):
    return omega_0**2/(omega_0**2-omega**2 + 2J*omega*zeta*omega_0)

omega_0 = 2*pi*1000
zeta = 0.1

Tomega = 2*pi*10**(linspace(2,4, 1001))
amplitude = H(Tomega, omega_0, zeta)

figure("exo1.1")
clf()
subplot(2,1,1)
title_str = 'Oscillateur amorti ($\omega_0/2\pi$={0} Hz et $\zeta={1}$)'
title(title_str.format(omega_0/(2*pi),zeta))
grid(True, which='both')
loglog(Tomega/(2*pi), abs(amplitude))
ylabel('Amplitude')
subplot(2,1,2)
semilogx(Tomega/(2*pi), angle(amplitude)/(2*pi)*360)
ylabel(u'Phase [°]')
xlabel(u'Fréquence [Hz]')
grid(True, which='both')

savefig('exo1_1.pdf')
savefig('exo1_1.png')

Tzeta = [.03,0.1,0.3,1]
Tlinetype = ['-', '--', '-.', ':']
figure("exo1.2")
clf()
for zeta, linetype in zip(Tzeta, Tlinetype):
    amplitude = H(Tomega, omega_0, zeta)
    loglog(Tomega/(2*pi), abs(amplitude), 'k'+linetype,
    label="$\zeta={0:4.2f}$".format(zeta), linewidth=2)
grid(True)
xlabel(u'Fréquence [Hz]')
ylabel(u'Phase [°]')
legend()
title_str = 'Oscillateur amorti ($\omega_0/2\pi$={0} Hz)'
title(title_str.format(omega_0/(2*pi)))
savefig('exo1_2.pdf')
savefig('exo1_2.png')

omega_0 = 2*pi*1000
omega_1 = 2*pi*2000

zeta_0 = 0.5
zeta_1 = 0.5

Tomega = 2*pi*10**(linspace(2,4, 1001))
amplitude = H(Tomega, omega_0, zeta_0)*H(Tomega, omega_1, zeta_1)

figure("exo1.3")
clf()
subplot(2,1,1)
title_str='Double oscillateur ($\omega_0/2\pi$={0} Hz,\
 $\zeta_0={1}$, $\omega_1/2\pi$={2} Hz et $\zeta_1={3}$)'
title(title_str.format(omega_0/(2*pi),zeta_0, omega_1/(2*pi), zeta_1))
grid(True, which='both')
loglog(Tomega/(2*pi), abs(amplitude))
ylabel('Amplitude')
subplot(2,1,2)

phase = angle(amplitude)
phase[phase>0] -= 2*pi
semilogx(Tomega/(2*pi), phase/(2*pi)*360)
ylabel(u'Phase [°]')
xlabel(u'Fréquence [Hz]')
grid(True, which='both')
savefig('exo1_3.pdf')
savefig('exo1_3.png')